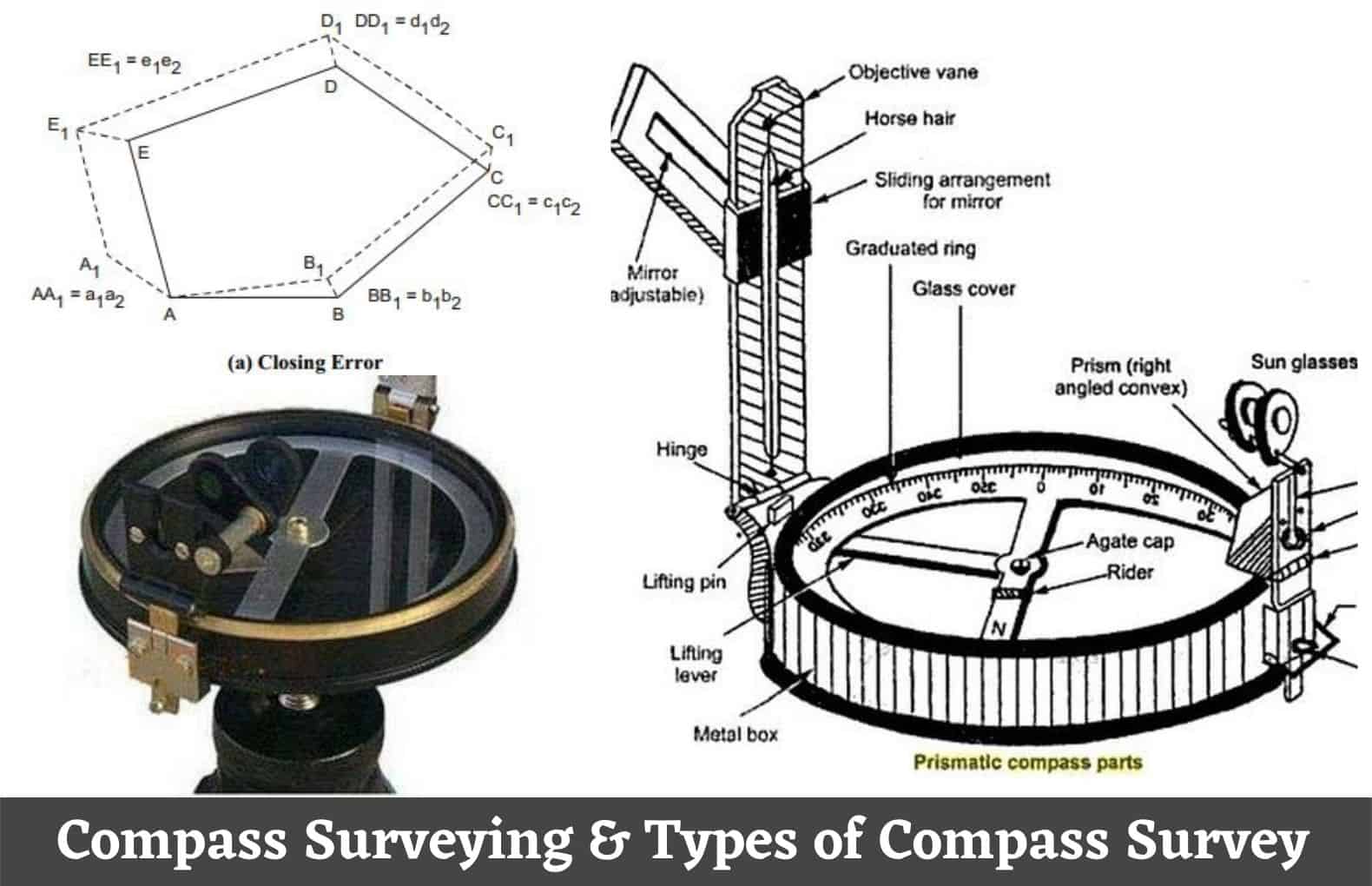
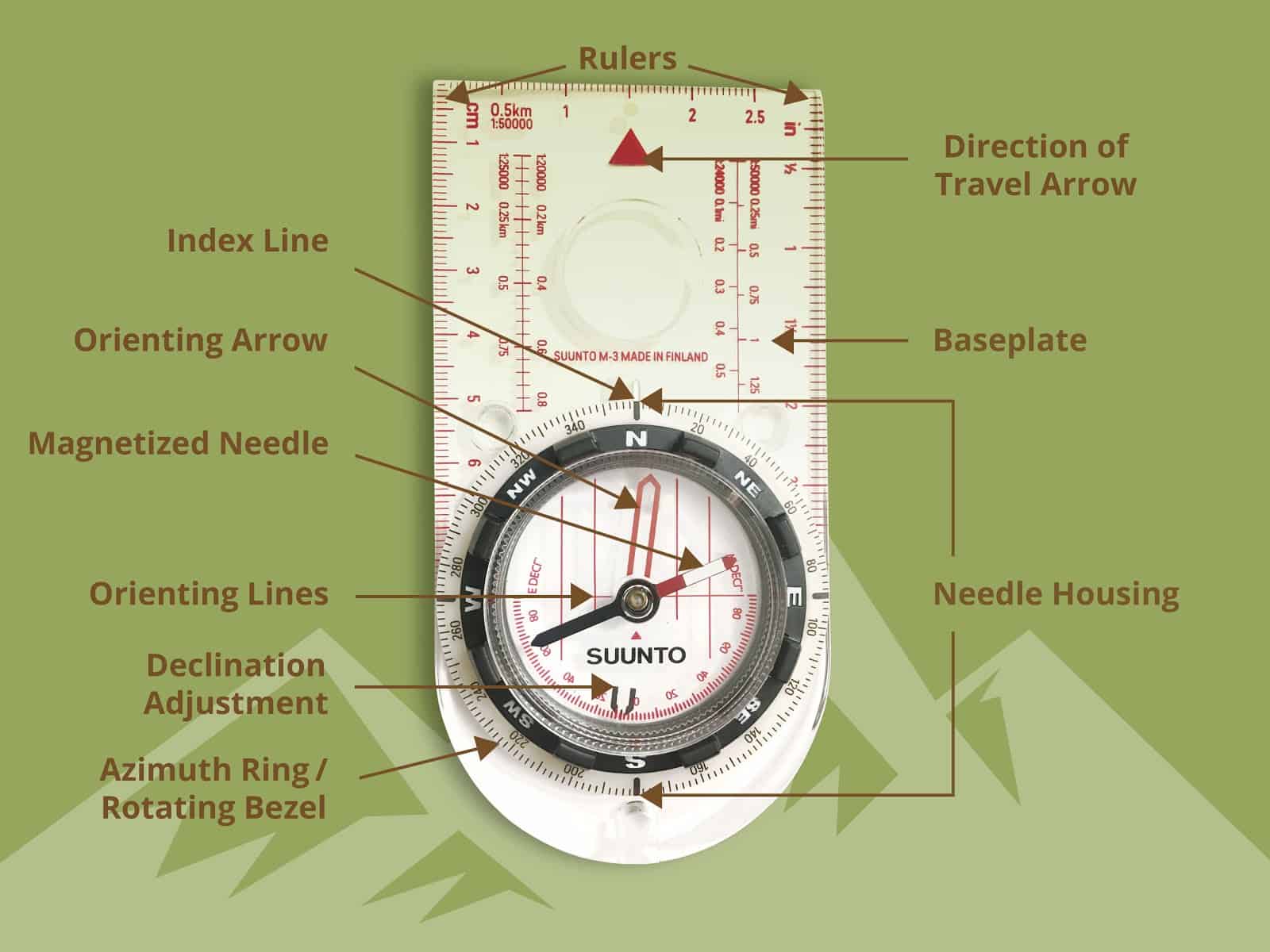
Step-by-step explanation:
If the compass width was changed, then we could not trace a bisecting line. Different arc measures would not intersect each other, at the center. So, we would not be able to trace a bisecting line.
When constructing an angle bisector the compass must be used to make three arcs do all three arcs need to have the same radius?
When an angle bisector is constructed, the compass must be used to draw three arcs and these three arcs do not need to have the same radius. So option C: 'no; any three radii will work' is the correct answer. In the context of geometry, an angle bisector refers to a line that splits an angle into two equal angles.
Which of these constructions is impossible using only a compass and straightedge?
Why must the compass point be placed on points A and B?
The compass must be placed at points A and B because the line given by them will intersect through the new point. You would receive random points of a perpendicular line. Step 3: Construct an angle and a perpendicular bisector.
What is a compass used for in construction?
In their different configurations, compasses are used for a variety of operations such as drawing, calculating proportions, measuring calibers, and determining positions at sea. Compasses with fixed points used in architectural design and construction work to record measurements and divide lines into equal parts.
Why do we use a geometric compass in geometry?
Compass is one of the mathematical tools which is used to draw a geometrical figure, such as a circle. It is also used in the intersection of line segments and tools, which is used to intersect the line segment and helps to find the midpoint of the shapes.
Why do construction workers use geometry?
Geometry is used to design with the best angles to make structures as strong as possible, using shape, size, position and other properties. Civil engineers use geometry to design and assemble shapes to construct freeways, tunnels, bridges and more.
Frequently Asked Questions
What kind of compass do I need for geometry?
I would recommend buying at least one 6-inch compass, a drop-bow compass for extra-small circles and a beam compass for big circles. If you want to know what they are used for and why, I've created a guide that includes everything you need to know about drawing compasses. You can download it here.
Why is the geometric compass important?
Galileo had invented a version of this geometrical compass a few years earlier and evidently gave copies of this manual to those who bought the compass. The compass had many uses, from performing square root calculations to determining ranges of cannons to solving surveying problems.
What are the advantages of drawing compass?
One of the advantages of using a compass is that it allows for the creation of perfectly symmetrical shapes and designs. By adjusting the distance between the point and pencil, the user can ensure that both sides of the shape are identical.
How do you double a square?
You can see it by adding lines. Right there you make those connections. The blue shape is a square all the sides are the same all the angles are the same. And it's half the area of the big square.
What happens to the area of a square when it is doubled?
It can be noticed that area of the square become four times when the side of the square is doubled.
How do you construct a square with two points?
From point B in on the right side and we're gonna do the same thing on the left. Side. So now we have two new intersection. Points here.
Is doubling a square possible?
3. Doubling a cube - impossible. 4. Doubling a square - possible.
What tools did Greeks use in geometric construction?
The two most important Euclidean tools used by early Greeks to construct different geometrical shapes and angles were a compass and a straightedge. Using these two tools, almost any shape can be constructed.
What tools are used when making geometric constructions?
Lesson Summary
When you draw something accurately without the use of numbers, it is called geometric construction. The two tools that you need to make geometric constructions are these two: compass, straightedge.
What tools did ancient Greece use for math?
The Greeks set up a particularly challenging set of rules when they formalized their notions of geometry. They restricted the set of tools that could be used for constructing figures to two instruments: a straightedge (with no markings on it) and a compass.
What tools did the Greek limit themselves to in their formal geometric constructions?
Ancient Greek mathematicians first conceived straightedge-and-compass constructions, and a number of ancient problems in plane geometry impose this restriction. The ancient Greeks developed many constructions, but in some cases were unable to do so.
What did the Greeks use for construction?
The upper elements of the temple were usually made of mud brick and timber, and the platform of the building was of cut masonry. Columns were carved of local stone, usually limestone or tufa; in much earlier temples, columns would have been made of wood.
Why are circles used in construction?
Their concept is an essential part of commercial architecture. The circle is considered one of the strongest shapes because stress is evenly distributed along the arc instead of concentrating it at one point. The interconnected points relieve it of upward pressure and give it lateral force.
What is the use of circles in engineering?
Engineering and construction: Circles are used in many engineering and construction projects, such as the design of bridges, arches, and domes. They are also used to create circular shapes in buildings and other structures, such as circular staircases, round windows, and circular fountains.
What is the circle in civil engineering?
What is the construction of the parts of a circle?
The parts of a circle are the radius, diameter, circumference, arc, chord, secant, tangent, sector and segment. A round plane figure whose boundary consists of points equidistant from a fixed point. The centre of the circle is the fixed point from which all points on the boundary of the circle are equidistant.
How important are circles in architecture?
Their concept is an essential part of commercial architecture. The circle is considered one of the strongest shapes because stress is evenly distributed along the arc instead of concentrating it at one point. The interconnected points relieve it of upward pressure and give it lateral force.
What was Taylor's major contribution was that he prized tradition and rules of thumb over knowledge and science?
Taylor's major contribution was that he prized knowledge and science over tradition and rules of thumb. He broke down each act of production into its smallest parts and watched the best workers perform their jobs.
What is the Taylor made management theory?
Essentially, Taylorism breaks tasks down into tiny steps, and focuses on how each person can do his or her specific series of steps best. Modern methodologies prefer to examine work systems more holistically in order to evaluate efficiency and maximize productivity.
What was a major contribution that Taylor made to the study of management?
One contribution of Frederick Taylor to management theory was that productivity would be increased through the optimization and simplification of work and not by forcing workers to work harder. He also proposed the cooperation between managerial executives and workers.
What are the 4 principles of management by Frederick Taylor?
What are the contributions of Taylor to organization effectiveness?
- Science, not a rule of thumb. Taylor advocated that employers ought to examine each element of a job scientifically.
- Harmony or cooperation between employer and workers.
- Scientific selection, and training and development of workers.
- Division of work.
How do you draw a line segment in construction?
- Take a ruler and mark a 0 point at one end the other point at the given length that is at 6 cm.
- Join the two points and so you a line segment of length 6 cm.
- Name the two end of the line segment as A and B respectively.
- The other way to draw the line segment is using a ruler and a compass.
How do you write construction in math?
Constructions are accurate drawings of shapes, angles and lines in geometry. To do this we need to use a pencil, a ruler (a straight-edge) and compasses. The basic constructions are perpendicular bisector and angle bisector.
What are classical construction tools in geometry?
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses.
What is a geometric drawing that uses a compass and a straight edge?
Which is used to draw line segments and to measure their lengths?
Ruler
A ruler is used to draw the line and to measure their lengths. Was this answer helpful?FAQ
- What are the only two tools we use for all our geometric constructions?
Lesson Summary
When you draw something accurately without the use of numbers, it is called geometric construction. The two tools that you need to make geometric constructions are these two: compass, straightedge.
- What are the basic instruments and devices in geometrical construction?
- Some of the most commonly used geometric tools are:
- Ruler.
- Compass.
- Protractor.
- Divider.
- Set-squares.
- What materials were used in Greek construction?
The upper elements of the temple were usually made of mud brick and timber, and the platform of the building was of cut masonry. Columns were carved of local stone, usually limestone or tufa; in much earlier temples, columns would have been made of wood.
- Which of the following is a step used in the construction of an equilateral triangle inscribed in a circle?
In Geometry, a step which is used in the construction of an equilateral triangle that is inscribed in a circle is drawing two (2) line segments which connect the two (2) points where the arc intersects the circle and an endpoint of the diameter.
- Which of the following is a step used to inscribe a square in a circle?
The following step that you would use to inscribe a square in a circle is: Construct an arc by placing the point of the compass on an endpoint of the diameter and the pencil on the center of the circle. The other steps are not used in drawing a square but in drawing other shapes.
- Can you draw a regular hexagon using only a straightedge and compass by first building an equilateral triangle?
- You can draw a regular hexagon using only a straightedge and compass by first building an equilateral triangle.
- Which of these tools or constructions is used to inscribe a hexagon inside a circle?
Expert-Verified Answer. The answer is a) equilateral triangle. If you want to inscribe a hexagon inside a circle, the tools or constructions that should be used is 6 equilateral triangles. If you draw a hexagon inscribed in a circle and draw radii to the corners of the hexagon, you will create triangles, six of them.
- How do you draw a triangle in a circle with a compass?
Circle. Next i'm going to indicate. Point d which is the intersection of the two circles at the top. And point e which is the intersection of the two circles at the bottom.
- How do you construct a right triangle with a compass?
We've made a perpendicular bisector. Now all we have to do is connect pb with a segment. And we've made a right triangle with a compass and a straight edge. So a real quick recap.
- What type of compass and straightedge construction?
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses.
- Which construction can you use to construct a right angle?
The construction of an angle of 90 degrees can be done in two ways - by using a compass and by using a protractor. Making a rough sketch is different from that of construction in geometry. In geometry, by construction, we mean drawing shapes, lines, angles with more accurate measurements.
- Which angle can be constructed with the help of compass and straight edge?
- 30∘,45∘,60∘,90∘,120∘ are some angles which can be drawn with the help of a ruler and compass.
- How to make a right triangle?
- Step 1: Draw a horizontal line of any length and mark a point C on it.
- Step 2: Set the compass width to 3 cm.
- Step 3: Place the pointer head of the compass on point C and mark an arc on both sides of C.
- How to do a translation in geometry with a compass?
The figure all right so it might be helpful to have this little transparency here so here's my vector. So our our strategy here is we're going to take this vector.
- What is the use of compass in geometry construction?
Compass is one of the mathematical tools which is used to draw a geometrical figure, such as a circle. It is also used in the intersection of line segments and tools, which is used to intersect the line segment and helps to find the midpoint of the shapes.
- How do you construct a reflection with a compass?
So you're looking for right here. If this was a and this is now going to be a prime you're going to use the same method for points b and c. So going to vertices b you're going to stretch.
- How to do rotations with compass?
And draw a little arc. And that's the path Point C is gonna take as it rotates around point P. But the question will be how far do you go when do you stop. And that's where we need this 90 degrees.
- How do you graph a translation in geometry?
- To graph the translation of a shape, we follow the steps below:
- Identify the vertices of the shape.
- Apply the given transformation on each of the vertices to find the new vertices (as shown in the above example).
- Then just plot the new points on the coordinate plane and join them as per the given shape.
- How do you construct a median with a compass?
Then we go over here to Y. And we do the same. Thing. Once that's in place and. Now we want to create another arc and again we're looking to find out where these two arcs intersect.
- How do you find the midpoint with a compass?
Open your contest so that the opening is more than half the length of the line. Place the point of the compass on the point a and draw a large arc that starts above the line. And ends below the line.
- How do you make a shape with a compass?
Today I'm gonna show you how to make the geometry for this basic hexagonal shape use a compass to draw the first circle. This is our base circle.
- How to construct an angle with a compass?
Then move it to this intersection.
- How do I construct a median?
A median of a triangle is a line segment from a vertex to the midpoint of the opposite side. This can be done by first constructing a perpendicular bisector on the side of the triangle opposite the desired vertex, and marking the point at which the bisector intersects the side of the triangle.
- How can a ruler be used to measure?
A ruler can be defined as a tool or device used to measure length and draw straight lines. A ruler is used to measure the length in both metric and customary units. The rulers are marked with standard distance in centimeters in the top and inches in the bottom and the intervals in the ruler are called hash marks.
- How do you measure objects with rulers?
Here we have an eraser. We want to measure its length. So we line up the zero of the ruler. Here reading along from zero we can see that we reach four so the length is four centimeters.
- How do you use a ruler compass?
Around. But for those of you that are new to this i would hold. The point the handle or the point down. And bring my pencil around and actually by just holding the point down i can just turn my paper.
How many compass settings are required to complete the construction?
| What is the ruler and compass construction? | In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an idealized ruler and a pair of compasses. |
| What is the use of ruler in carpentry? | The ruler is used to find the middle of an edge by placing it across the piece so that the distances from the edges of the piece to corresponding fractional marks, shall be the same. The middle of the piece being at a point midway between the marks selected. |
| How do you divide a hexagon into 5 equal parts? | Simply divide the hexagons perimeter into 5 equal parts and connect to the center point. For example if each side is 1 inch, start at a vertex go to the next vertex of one inch and go 1/5 of an inch into the next side. |
| Are all hexagons congruent? | The regular hexagon has all side lengths with the same measure. The irregular hexagon does not have sides that are the same length. The answer is no, the two hexagons are not congruent as their corresponding sides are not all the same measure. |
| Can three congruent regular hexagons be drawn in such a way? | Yes, it is possible to draw three congruent regular hexagons in such a way that they overlap each other and create more than 6 distinct areas or compartments. When the three hexagons are arranged in a certain way, they can form a larger hexagon with many smaller hexagons inside. |
| How many segments are in a hexagon? | Six line segments Hence, a polygon formed by six line segments is called Hexagon. |
| What is a hexagon with 5 sides called? | A pentagon is a polygon with 5 sides and 5 angles. |
| What geometric instrument would I use to measure the length of a segment? | A protractor is used to measure the length of a line segment. |
| How do you measure the length of a line segment? | Answer: The length of a line segment can be measured by measuring the distance between its two endpoints. It is the path between the two points with a definite length that can be measured. Explanation: On a graph, the length of a line segment can be found by using the distance formula between its endpoints. |
| Which instrument is used to construct line segment? | To construct a copy of a given line segment, we can use either a ruler or a compass. Q. 70∘ can be constructed using a ruler and a compass. |
| Which instrument do you use to measure the length of line? | A scale or ruler is an instrument used to measure distance. A divider is also used to measure distance but with more accuracy. |
| How do you measure segments in geometry? | To find the measure or size of a segment, you simply measure its length. What else could you measure? After all, length is the only feature a segment has. You've got your short, your medium, and your long segments. |
| What constructions is impossible using only a compass and straightedge? | Angle trisection is the construction, using only a straightedge and a compass, of an angle that is one-third of a given arbitrary angle. This is impossible in the general case. |
| What is the compass and straightedge problem? | Compass and straightedge constructions are a class of problems in classical geometry. They take the form "Using only a compass and a straightedge, construct X", where X is a geometric figure such as a regular pentagon. The subject is typically covered in high school mathematics. |
| Who made the rule that a ruler and a pair of compasses only should be used for geometrical construction? | The notion of ruler and compass construction was a theoretical one to the Greeks. A ruler was taken to be an object that could draw perfect, infinitely long lines with no thickness but with no markings to measure distance. The only way to use a ruler was to draw the line passing through two points. |
| How are a straightedge and compass used to make basic construction? | The straightedge is used to draw the line (or line segment) between any two points. The compass can be used to draw circles (or circular arcs) with center at a given point, passing through any other point. But it can also be used to duplicate lengths. |
| What 3 classic geometric problems cannot be solve with straightedge and compass alone? | Such construc- tions lay at the heart of the three classical geometric problems (1) squaring the circle (also known as quadrature of the circle), (2) duplicating the cube, and (3) trisecting an arbitrary angle. The Greeks were unable to solve these problems. |
| Why is it better to use a compass and straightedge? | Compass and Straight Edge Constructions. Compass and straightedge constructions are foundational techniques that have been used for millennia. With these tools, one can create precise shapes and figures without the need for numerical measurements. |
| What are the benefits of using a compass and straightedge over technology? | First of all it's more accurate, faster, clearer/cleaner(drawing) and if you did it right then it's going to be perfect. What are the limitations to using technology over a handheld compass and straightedge? Using technology doesn't allow your creative juices to flow as freely and requires less brain work. |
| How are a straightedge and compass used to make basic constructions? | The straightedge is used to draw the line (or line segment) between any two points. The compass can be used to draw circles (or circular arcs) with center at a given point, passing through any other point. But it can also be used to duplicate lengths. |
| Why should students use a compass and a straightedge instead of a drawing program? | And drawing programs do have accuracy limitations, which are sometimes worse than those of a straight-edge and compass. Floating point numbers are quantized, and not especially consistently. Many drawing programs only pretend to draw arcs and circles. They actually draw regular polygons instead. |
| What is the advantage of using a compass to navigate? | Using a compass with a map gives a broader geographical context, helps you remember the route and learn about other things on the way. A compass and map are more reliable but require a higher level of navigational skill and understanding and should always be carried on a trek. |
| What is the age of geometry? | The earliest recorded beginnings of geometry can be traced to early peoples, such as the ancient Indus Valley (see Harappan mathematics) and ancient Babylonia (see Babylonian mathematics) from around 3000 BC. |
| Is regular 7 Gon constructible? | ∴ Regular 7-gon is not constructible. (with twice the degree) with coefficients in F. |
| What are the 4 basic constructions in geometry? | The Six Basic Constructions
|
| What is the history of the geometrical compass? | The geometric and military compass of Galileo belonged to this class of instruments. Invented in Padua in 1597, the instrument is also linked to Galileo's activity (fig. 7) in the Accademia Delia (fig. 8), founded in Padua to provide mathematical instruction for young noblemen training for a military career. |
- Is it possible to trisect an angle using only a compass and straightedge?
This problem was finally solved in 1837 by Pierre Wantzel: the reason that no one has ever managed to trisect the angle with only compass and straightedge is that it is impossible to do so.
- Which of the following constructions were never accomplished by the Greeks with only a straightedge and compass?
Actually there are three types of construction that were never accomplished by Greeks using compass and straightedge these are squaring a circle, doubling a cube and trisecting any angle.
- How are straightedge and compass used to make basic constructions?
The straightedge is used to draw the line (or line segment) between any two points. The compass can be used to draw circles (or circular arcs) with center at a given point, passing through any other point. But it can also be used to duplicate lengths.
- Why use a compass and straightedge in geometry?
With these tools, one can create precise shapes and figures without the need for numerical measurements. One of the intriguing tasks is constructing a trapezoid using only a compass and straightedge. This technique requires a keen understanding of geometric principles and a steady hand.
- Which angles Cannot be drawn using compass?
With a ruler and compass we can construct 15∘, 30∘, 45∘, 60∘, 75∘, 90∘, 105∘ angles. We cannot however construct an 80∘ angle with a ruler and compass only.
- How could you use the construction tool or a compass and straightedge to create a line segment that is twice as long as?
Measure the length of AB by using a compass. Then, keeping the compass at that length, use the straightedge and compass to draw a copy of AB. Move the compass to the endpoint of AB to draw a second copy of AB, keeping the straightedge in the same place. This line segment is now a distance of 2AB.
- How do you copy a line segment using a compass and straightedge?
And use our a over here as the center of the circle. And then draw an arc to find the intersection. Between our circle. And the line we originally drew okay so that intersection is our point B.
- When constructing parallel lines with a compass and straightedge How should you start construction?
When constructing parallel lines with a compass and straightedge, how should you start the construction? Measure the length of the original line and make an arc. Create a line that intersects the given line with your straightedge. Open the compass to the width of the line and draw two arcs.
- How would the construction be different if you change the compass setting in the next step of the perpendicular bisector construction?
A perpendicular bisector divides a line segment into two equal segments. If the compass setting is changed, the line will not be bisected.
- Which angles can be drawn with compass?
Another method of constructing angles is by using a compass and a ruler. But we can use this method to construct some particular angles only such as 60°, 30°, 90°, 45°, etc. We can construct angles line 23°, 44°, 57°, etc., with accuracy using a compass and ruler.
- What is the construction of a compass?
Magnetic compasses consist of a magnetized needle that is allowed to rotate so it lines up with Earth's magnetic field. The ends point to what are known as magnetic north and magnetic south.
- How do you make an arc with a compass?
So there's an arc. And I put it kind of on the side. So you can see that it works in any which way and you find the two points of the arc point a and point B. So now you grab a pen and a compass.
- Which angles Cannot be drawn by compass?
With a ruler and compass we can construct 15∘, 30∘, 45∘, 60∘, 75∘, 90∘, 105∘ angles. We cannot however construct an 80∘ angle with a ruler and compass only.
- What angles can be constructed?
- Types of Angles for Construction
- Acute angle (less than 90 degrees)
- Obtuse angle (more than 90 degrees)
- Right angle (exactly 90 degrees)
- Straight angle (equal to 180 degrees)
- Reflex angle (more than 180 degrees)
- Full rotation (equal to 360 degrees)
- Types of Angles for Construction
- How do you construct an angle bisector?
- How Do You Construct an Angle Bisector?
- Step 1: Draw an angle of any measure.
- Step 2: With one end of the horizontal ray which makes the angle as the center and measuring any width (less than the length of the ray drawn) in the compass, draw an arc that intersects the two rays of the angle at any two points.
- How Do You Construct an Angle Bisector?
- How many angles we can make with compass?
The simple answer is infinitely many because any angle you can construct can be bisected as many times as you want. You can also add any two angles that you can construct.
- What does a compass draw?
A compass is an instrument that is usually a metal or plastic V-shaped drawing tool. It majorly consists of two movable arms, which are hinged together. It is used to draw circles or the parts of circles called arcs. A compass is also called a pair of compasses.
- What is the postulate 5 in geometry?
If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
- What is postulate 1?
GEOMETRY POSTULATES AND THEOREMS
Postulate 1: Through any two points, there is exactly one line. Postulate 2: The measure of any line segment is a unique positive number. The measure (or length) of AB is a positive number, AB.
- What is postulate 4?
That all right angles equal one another.
- What is Proposition 2 in geometry?
- To place a straight line equal to a given straight line with one end at a given point. Let A be the given point, and BC the given straight line. It is required to place a straight line equal to the given straight line BC with one end at the point A.
- What is postulate 7 in geometry?
GEOMETRY POSTULATES AND THEOREMS
Postulate 7: If two points lie in a plane, then the line joining them lies in that plane. Theorem 1.1: The midpoint of a line segment is unique. Postulate 8: The measure of an angle is a unique positive number.
- Why do Euclidean geometric constructions only permit the use of a straightedge and compass when more powerful tools were already available in ancient times?
The real reason is probably that straightedge and especially compass are the simplest, most primitive instruments, and also easy to make. At the same time they are quite accurate.
- Why is it important to use a compass and straightedge?
Nowadays, although different constructions can be made with various tools such as computer software, protractor, etc., constructions made with a compass and a straightedge are important because they force comprehension of the geometric constructions in the mind (Sezen, 2007).
- How do you construct an angle bisector with a compass?
To make two more arcs. So I'm going to go back here. Okay. I'm gonna make an arc.
- What are the steps for constructing a copy of an angle using only a compass and a straightedge?
- Start with a angle BAC that we will copy.
- Make a point P that will be the vertex of the new angle.
- From P, draw a ray PQ.
- Place the compasses on point A, set to any convenient width.
- Draw an arc across both sides of the angle, creating the points J and K as shown.
- Start with a angle BAC that we will copy.